Fibonacci的优化思考

Fibonacci是一种经典的算法，它的解法从递归、递推到列通项公式的推导都可以完成，它使用了分治的思想——把目标问题拆为若干个小问题，利用小问题的解得到目标问题的解。

递归求解

递归是最容易想到的写法，它的好处就是代码清晰明了，总的计算量近似可以等于高度为n-1的二叉树的节点总数，所以它的时间复杂度为O(2^n)

def fib(n):
    assert n >= 0, 'input invalid'
    return n if n<=1 else fib(n-1) + fib(n-2)

存在问题

先看一张图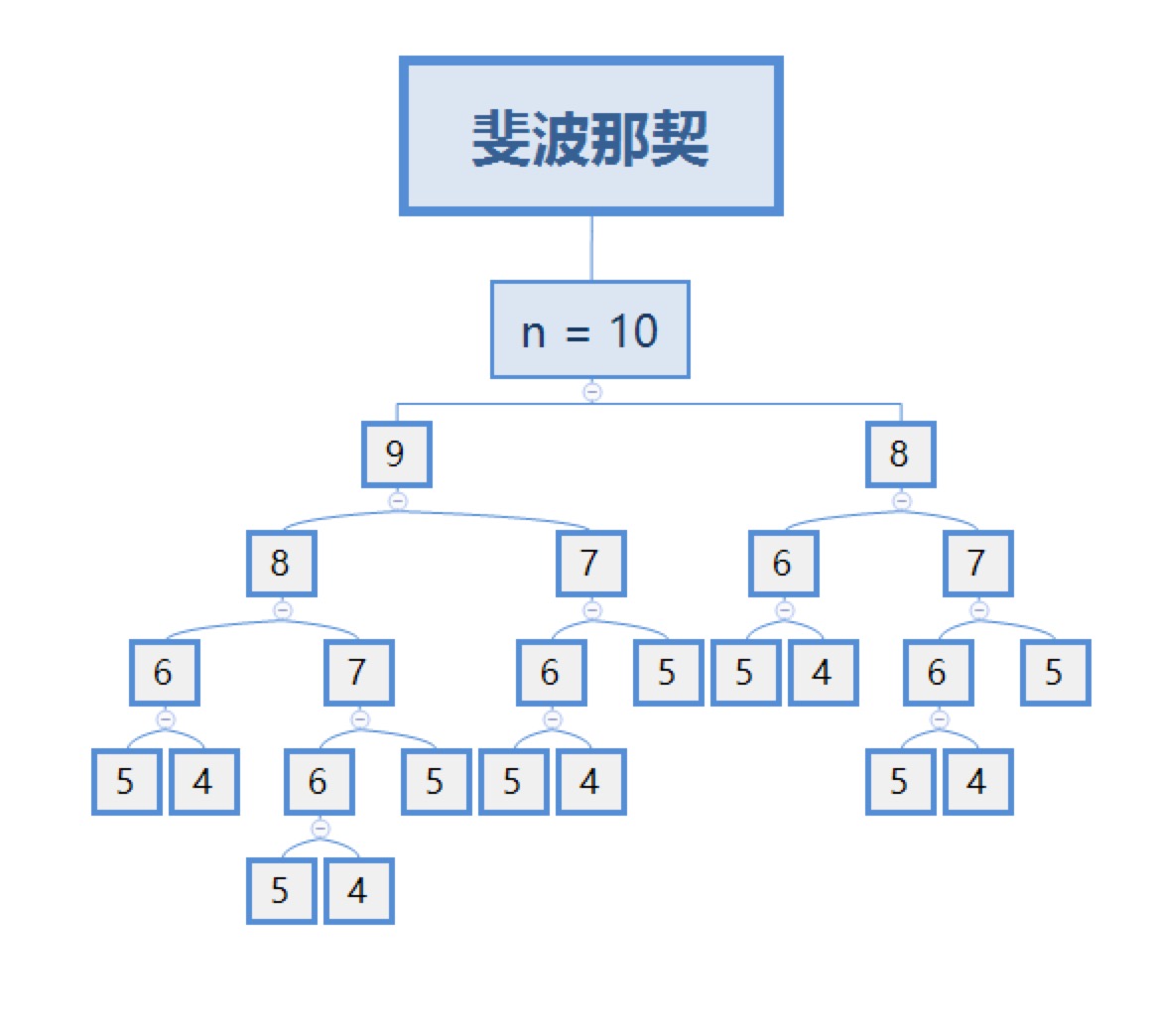： Fibonacci_in_BTree 这张图说明了Fibonacci计算过程中的计算每一个节点时需要计算的节点的量，可知有很多重复节点的计算，如计算F(9)时需要计算F(8)和F(7），而计算F(8)时又计算了一次F(7) ，所以这里存在优化的空间。

加入缓存

def fib(n, cache=None):
    if cache is None:
        cache = {}
    if n in cache:
        return cache[n]
    if n == 1 or n == 0:
        return 1
    else:
        cache[n] = fib(n - 2, cache) + fib(n - 1, cache)
        return cache[n]
print([fib(n) for n in range(999)])

通过cache机制，使得每次计算之前先判断是否已经存在，从而避免了多次重复计算。

递推求解

递归的一个问题就在于，如果层数很深，那么它的时间复杂度会指数级上升，性能显著下降并且可能会报错maximum recursion depth exceeded，所以一般也不会采用递归的方式求解。递推的方式效果就会好很多，我们可以把斐波那契的前两项先初始化为数组，然后根据f(n) = f(n-1) + f(n-2) 用循环一次算出后面的每一项，这种算法的时间复杂度为O(n)。

迭代器实现

class Fibs:
    def __init__(self):
        self.a = 0
        self.b = 1

    def next(self):
        self.a, self.b = self.b, self.a + self.b
        return self.a

    def __iter__(self):
        return self

这将得到一个无穷的数列，可以采用如下方式访问：

fibs = Fibs()
for f in fibs:
    if f > 1000:
        print(f)
        break
    else:
        print(f)

每次迭代计算会依次向后计算一个值，这样就避免了重复计算。

数组实现

def fast_fib(n):
    f = [0, 1]
    for i in range(2, n+1):
        f.append(f[i-1] + f[i-2])
    return f[n]

思路和迭代器一样，每次计算都拿现成的两个值直接进行加法即可，运算效率高。这里的数组是动态扩容的，相当于Java中的List集合。

边界问题

在斐波那契数列中，设计终止递归循环的边界是可以随意的，只要符合斐波那契数列的计算逻辑：

终止条件中的n的最小值要大于等于0，小于0没有任何意义，并且不符合斐波那契规则，造成不可估量错误。
要包含当n为基数以及偶数两种情况下n的返回值，主要是因为递归调用时有f(n-1)和f(n-2)，那么就一定有奇偶数两种情况。

例子：可以设计为在n=6时返回8，在n=7时返回13。

public static int fibo(int n) {
    if (n == 6) {
        return 8;
    } else if (n == 7) {
        return 13;
    } else{
        return fibo(n - 1) + fibo(n - 2);
    }
}

调用时传入参数n的最小值不能小于终止判断条件的最小判断值：本例子中规定了n必须大于6。

本文首次发布于 LiuShuo’s Blog, 转载请保留原文链接.

Fibonacci Optimization